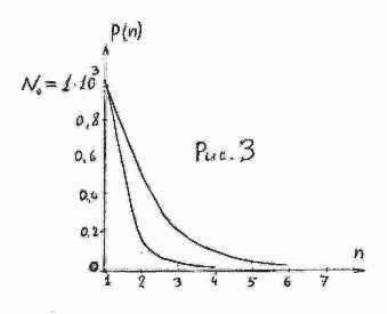
Рис.3. Зависимости числа фотоотсчетов в сек. от кратности импульсов, вычисленные по формулам (7) - кривая I, и (8) - кривая II, для случая Nf =0,1 представлены на рис.3. Число единичных фотоотсчетов в сек. в обоих случаях положено равным 1000.

Корпускулярно-волновой дуализм и закон сохранения энергии. Л.Р.
http://www.newsland.ru/news/detail/id/848468/
ВОПРОС О РЕАЛЬНОСТИ ВОЛНОВОЙ ФУНКЦИИ СТАВИТСЯ НА ПОВЕСТКУ ДНЯ (Л.Р.)
ВОПРОС О РЕАЛЬНОСТИ ВОЛНОВОЙ ФУНКЦИИ СТАВИТСЯ НА ПОВЕСТКУ ДНЯ (Л.Р.)
Составлен рейтинг самых популярных научных открытий 2011 года
Открытие трио физиков во главе с Мэтью Пьюзи из Imperial College в Лондоне: волновая функция, одна из основ теории квантовой механики, может быть наблюдаемым физическим явлением, а не только теоретическим концептом, каковым его считали многие ученые. Эта функция использовалась прежде для описания "чистого состояния системы". Хотя непосвященным сложно понять, в чем здесь дело, специалисты говорят, что превращение волновой функции из чисто статистического понятия в нечто реально существующее потрясает сами основы квантовой теории. Эта непростая для понимания "дилетантами" новость заняла шестое место.
БОЛЕЕ ПОДРОБНО СМ. В АНГЛИЙСКОЙ ЧАСТИ САЙТА
БОЛЕЕ ПОДРОБНО СМ. В АНГЛИЙСКОЙ ЧАСТИ САЙТА
Гипотеза Эйнштейна о корпускулярной природе электромагнитного излучения, выдвинутая им в качестве "эвристической точки зрения" для объяснения законов фотоэффекта, впервые поставила вопрос о сочетании в одном объекте волновых и корпускулярных свойств. После того, как идея Де-Бройля о волновой природе электрона была подтверждена экспериментами Дэвиссона-Джермера, проблема корпускулярно-волнового дуализма приняла универсальный характер. Противоречие между понятиями пространственно протяженного поля и пространственно локализованной частицы оказалось настолько глубоким, что возникла целая философская школа, которая вообще отказалась от классического способа описания физического объекта как реальности в пространстве и времени, не зависящей от приборов, используемых для наблюдения. В поисках реалистического выхода из создавшегося положения наметились два основных пути: Де-Бройль и Бом считали необходимым сохранить понятие локализованной частицы (корпускулы) в числе основных понятий теории, тогда как Планк и в особенности Шредингер отстаивали монистическую волновую картину.
Первый путь оказался связанным с искусственностью теоретических предпосылок и привел к большим математическим трудностям. Второй путь представляется более конструктивным, так как успешно работающий математический аппарат квантовой физики соответствует именно волновой картине: корпускулярный аспект появляется только в процессе интерпретации. Однако сразу же возникает вопрос: может ли реалистическая волновая картина быть согласована с простейшими экспериментальными фактами? Мы в данной работе приходим к выводу, что такое согласование возможно только в том случае, если предположить экспериментально наблюдаемое нарушение законов сохранения энергии и заряда в единичных взаимодействиях.
Планк указал на парадокс, возникающий при чисто волновой концепции электромагнитного излучения. Пусть на какой-либо удаленной звезде атом испускает единичный волновой цуг, ограниченный во времени и имеющий некоторый угол расхождения α. В момент наблюдения волновой цуг будет иметь ширину фронта αL, где L – расстояние до звезды. Нет никаких оснований полагать, что эта ширина может быть чем-то ограничена. Во всяком случае, экспериментальным фактом является то, что эта ширина не меньше максимальной базы звездного интерферометра Майкельсона, достигающей 20 м и более. А современные методы наблюдения, использующие интерференцию между двумя удаленными телескопами, доказывают, что ширина фронта световой волны не меньше расстояния между этими телескопами.
Пусть для наблюдения используется фотоэлемент с потенциалом выхода U(ν). Предположим, что один эмиттирующий электрон собирает энергию излучения с площади взаимодействия sО, равной по порядку величины площади единичного электронного цуга внутри кристаллической решетки фотослоя (в некоторых случаях это размер монокристалла). Если же эмиттирует не свободный, а связанный электрон, то Sо совпадает с площадью внешней оболочки атома. Можно взять излучение настолько малой интенсивности, что энергия еU(ν) сможет быть накоплена электроном только в течение нескольких минут после начала облучения. Хотя вопрос о промежутке времени между началом облучения и началом фотоэлектронной эмиссии, насколько мы знаем, экспериментально не изучался, однако ясно, что этот промежуток очень мал и не имеет никакого отношения ко времени накопления энергии, рассчитанному по классической теории электромагнитного поля. Более того, оказывается, что каждый электрон под действием излучения приобретает всегда одинаковую энергию, равную hν.
Примечание автора 2009 г.: в настоящее время я считаю это утверждение ошибочным, что обесценивает выводы этой статьи о непременной связи волновой картины с нарушением закона сохранения энергии в единичных взаимодействиях. Однако другие рассуждения, вытекающие из предположения о чисто волновой природе поля, т.е. о несуществовании такой вещи как фотон, остаются справедливыми, несмотря на эту ошибку. Данная статья стала для меня только первым этапом формирования волновой концепции поля, свободной от корпускулярно-волнового дуализма.
Если одновременно сохранить понятие поля и понятие энергии поля, распределенной в пространстве (с плотностью, пропорциональной квадрату амплитуды), то придется предположить, что энергия hν, полученная единичным волновым цугом в акте излучения и распределенная по всему объему цуга, должна практически мгновенно локализоваться в области, в которой происходит передача всей этой энергии электрону детектора. Таким образом, мы приходим к нарушению принципа близкодействия.
Отсюда следует, что три основных начала классической теории поля: пространственно - временная реальность, энергия и близкодействие перед лицом экспериментальных фактов не могут быть сохранены одновременно. По крайней мере от одного из этих начал необходимо отказаться.
Отказ от описания поля как объективной реальности в пространстве и времени характерен для копенгагенской интерпретации квантовой теории. При этом в несколько модифицированном виде сохраняются как понятие энергии, так и принцип близкодействия, во всяком случае, пока речь идет об экспериментально наблюдаемых выводах теории. Предполагается, что единичный цуг электромагнитного поля может вызвать появление только одного фотоэлектрона в какой-либо точке из области, где амплитуда ψ–функции «фотона» отлична от нуля, и при этом вся энергия одного фотона действительно передается одному электрону.
Согласно копенгагенской концепции, при переходе фотона из состояния с определенным импульсом в состояние с определенной координатой происходит мгновенная «редукция волнового пакета». Однако принцип близкодействия этим не нарушается, поскольку ψ–функция (точнее |ψ|²) отнюдь не описывает реальное поле, но представляет собой лишь функцию распределения вероятностей обнаружения фотона в различных точках пространства-времени. Реальное же нарушение принципа близкодействия, т.е. передача сигнала со скоростями, превышающими скорость света, не предусматривается ни в одном из следствий современной квантовой теории. Возможность отказа от принципа близкодействия с целью сохранения понятий поля и энергии рассматривалась некоторыми физиками, но никто из них, насколько нам известно, не смог доказать эту гипотезу экспериментально.
Примечание автора 2009 г.: ни одна из попыток такого рода до сих пор не увенчалась успехом – во всех этих экспериментах речь всегда идет о косвенных умозаключениях, но не о реальной передаче сигнала.
Остается третья возможность – сохранение понятий поля и принципа близкодействия ценой отказа от понятия энергии. К этой мысли был очень близок Шредингер, постоянно указывавший на необходимость пересмотра понятия энергии [1]. Сразу же оговоримся, что мы здесь не имеем в виду нарушение законов сохранения квантовомеханических величин, определяемых как собственные значения соответствующих операторов. Хотя собственным значением оператора Гамильтона является величина hν, однако в процессах взаимодействия фотонных и электронных волн (излучение, фотоэффект, эффект Комптона) постоянная Планка во многих случаях вообще не фигурирует, ибо правые и левые части уравнений можно сократить на h. Например, для фотоэффекта имеем:
νe = νf /1/
т.е. частота испущенной электронной волны равна частоте падающей фотонной волны, так что здесь можно говорить не о законе сохранения энергии, а о законе сохранения частоты.
Постоянная Планка нетривиальным образом появляется лишь в уравнении Шредингера, определяющем закон изменения длины волны для электронных волн в потенциальном (главным образом – электростатическом) поле:
λe = h/√[2hνf – (Ur+Ui)] /2/
где Ui – потенциал выхода, Ur – потенциал внешнего поля.
Мы предполагаем, что уравнения (1) и (2) должны оставаться неприкосновенными, но в то же время отказываемся видеть в величине hν нечто большее чем просто частоту, умноженную не некоторую константу, входящую в закон взаимодействия полей.
Как же в таком случае обстоит дело с приведенным выше парадоксом Планка? Если мы хотим сохранить понятие реального поля и в то же время не подвергаем сомнению принцип близкодействия, то мы будем вынуждены предположить, что цуг фотонной волны частоты ν, испущенный атомом в единичном акте излучения, может вызвать появление сразу нескольких фотоэлектронов, или, точнее, единичных цугов электронных волн, в разных точках фронта падающей волны. Хотя все цуги подчинены соотношениям (1) и (2), однако закон сохранения энергии при этом нарушится, ибо "один фотон" может вызвать появление одновременно "нескольких фотоэлектронов", каждый из которых, по существующим воззрениям, несет энергию hν.
Примеч. 2009: как уже указывалось выше, в настоящее время я считаю это утверждение ошибочным.
Действительно, согласно принципу близкодействия, в акте испускания электронной волны могут принимать участие только те элементы падающей фотонной волны, которые находятся в непосредственной близости от области взаимодействия. Удаленные же части падающей волны не могут ничего "знать" о происшедшем событии и, следовательно, такое же событие может одновременно произойти и в других областях пространства, в которых амплитуда данного волнового цуга отлична от нуля.
Утверждая, что амплитуда A (x,t) падающей волны есть амплитуда реального физического поля, мы в то же время вынуждены предположить, что |A (x,t) |² пропорциональна вероятности взаимодействия в данной точке; при этом мы не можем в каждом случае предсказать, произойдет или не произойдет это взаимодействие в действительности. Поэтому единичный волновой цуг в некоторых случаях вообще не вызовет эмиссии электрона, а в других случаях может вызвать эмиссию сразу нескольких электронов.
Изменение в математическом аппарате квантовой теории, вносимое представлением о реальности волнового поля, заключается лишь в том, что условие нормировки перестает быть тривиальным и поэтому в теории должно фигурировать абсолютное значение амплитуды, а не только ее относительное значение, как это имеет место в современной квантовой механике. Таким образом, теория должна объяснить, почему одному единичному цугу фотонной волны соответствует один единичный цуг электронной волны, т.е. почему интеграл ∫|A (x,t) |² dxdt по всему объему волнового цуга есть величина, в среднем сохраняющаяся при взаимодействии.
Далее, из уравнений теории должно вытекать следствие о тенденции полей атомных ядер и других волновых полей высокой частоты к локализации в компактные и достаточно устойчивые волновые пакеты, существование которых неоспоримо доказывают эксперименты по рассеянию и треки в камере Вильсона или в фотоэмульсии. При этом, поскольку, например, атомные ядра одного вида с высокой степенью точности являются одинаковыми (при одной и той же скорости они оставят одинаковые треки), то соответствующие волновые пакеты должны иметь одинаковый пространственный размер и одинаковую нормировку. Поскольку нуклоны состоят из кварков, то это условие переносится на них. Таким требованиям может удовлетворить только нелинейная теория, включающая в себя одну или несколько констант размерности длины, ибо волновые пакеты должны "знать", относительно какого естественного масштаба они определяют свои пространственные размеры.
Можно предложить ряд простых экспериментальных схем для проверки законов сохранения энергии и заряда в единичных взаимодействиях.
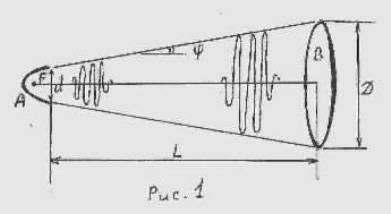
Свет от слабого источника F с регулируемой мощностью отражается параболическим зеркалом А и собирается в пучок с начальным диаметром d и углом расхождения φ . На расстоянии L от источника помещено входное окно детектора квантов. Если диаметр экрана D удовлетворяет условию:
D > d + L tg φ /3/
то каждый волновой цуг, испущенный в акте испускания атома (будем называть его: «единичный цуг», «квант» или «фотон»), целиком попадет на экран. Интенсивность источника уменьшается до тех пор, пока не будет выполнено условие:
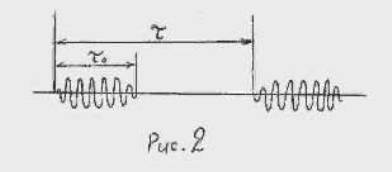
τо<<τ
где τо - длительность единичного волнового цуга, τ - среднее значение промежутка времени между двумя последовательными цугами (рис.2).
Рассмотрим вероятность того, что из фотокатода будет выбито одновременно n фотоэлектронов, положив пока для простоты, что квантовый выход фотоэффекта составляет 100% (один электрон на один квант). Разрешающую способность системы отсчета импульсов фототока положим равной ∆t. Система отсчета должна различать импульсы по амплитуде, т.е. различать импульсы, соответствующие 1,2... n фотоэлектронам.
Для источника света с пуассоновским распределением цугов, вероятность того, что за время ∆t на окно детектора попадет n цугов, равна:
PN = Nfⁿ exp(-Nf)/n! /4/
где среднее количество цугов, попадающих на детектор за время ∆t:
Nf = ∆t/τ
Очевидно, что при Nf>>1 нельзя выяснить, бывают ли случаи, когда один единичный цуг вызывает эмиссию двух и более электронов, поскольку этот эффект, если он существует, будет полностью замаскирован наложением цугов друг на друга.
Ситуация в корне меняется, когда среднее количество квантов, приходящих за время ∆t, становится много меньше единицы:
Nf << 1
В некоррелированных источниках испускание каждого цуга есть независимое событие, и вероятность наложения n цугов в течение времени ∆t равна:
P(n) = Nfⁿ /5/
Если квантовый выход детектора равен 100% и потери отсутствуют, то эта формула определяет также вероятность появления одновременно n первичных электронов на фотокатоде и соответственно наблюдения выходного сигнала с соответствующей амплитудой. Путем уменьшения Nf, т.е. интенсивности источника света, вероятность наблюдения двухэлектронных импульсов на выходе детектора может быть сделана сколь угодно малой.
Совершенно другое распределение n-электронных импульсов имеет место, если справедливы принцип реальности и принцип близкодействия. В этом случае в качестве независимых событий следует рассматривать выбивание фотоэлектронов на разных участках одного и того же единичного волнового цуга.
Площадь такого участка, на котором происходит реальное взаимодействие светового поля с отдельным электроном, обозначим как Sо. Для твердотельного детектора эта площадка не может быть больше единичного монокристалла. Во всех практически значимых случаях будет соблюдаться условие Sо << S, где S – рабочая площадь детектора.
Вероятность появления n-электронного сигнала на выходе определяется в этом случаем возможностью выбивания двух и более фотоэлектронов одним и тем же единичным цугом. Поскольку нет никаких причин сомневаться в том, что закон сохранения статистически выполняется, то среднее значение фотоэлектронов на один квант должно быть равно 1. В результате вероятность наблюдения n-электронного сигнала определится формулой Пуассона со средним значением 1:
P = 1/en! /6/
При Nf>>1 формула (6) должна быть заменена на (4), поскольку начинает преобладать вероятность взаимного наложения цугов.
Если сравнить отношения вероятностей для n-кратных и к-кратных импульсов, вычисленных из (4) и (6), то получим, в первом случаe:
PN(n)/PN(k)= Nf R(n-k)[k!/n!] /7/
(здесь R означает показатель степени),
а во втором:
P(n)/P(k)= k!/n! /8/
Например, для Nf =0,1; n=2; k=1 выражение (7) дает:
P0,1(2)/P0,1(1)= 0,05
тогда как из (8) получаем:
P(2)/P(1)= 0,5
Характерной особенностью выражений (6) и (8) является независимость от Nf, т.е. от интенсивности падающего света.
Проф. Arecchi (Universita di Milano) в 1965 году провел эксперименты [2] по изучению зависимости скорости фотоотсчетов от числа электронов в импульсе для лазерного и для искусственного гауссова источника. В соответствии с поставленной задачей он положил Nе = 1,2–1,4 что при квантовом выходе 10% соответствует 12–14 световым цугам в течение времени ∆t. Разрешающее время ∆t=(0,5 – 10) х 10(-4) сек. обеспечивался вращением диска с отверстиями. Для того, чтобы эти опыты могли служить проверкой волновой или корпускулярной природы света и одновременно закона сохранения энергии в единичных взаимодействиях, необходимо на два порядка снизить интенсивность падающего света или в такой же степени уменьшить разрешающее время ∆t. Уменьшение ∆t предпочтительно, поскольку при этом улучшается отношение полезного сигнала к шумам детектора.
Отказавшись от условия /3/, Рассмотрим обобщение формул (5)-(8) для случая, когда на входное окно детектора попадает только часть волнового цуга, определяемая параметром m. Если амплитуда во всех точках цуга приблизительно одинакова, то
m = S/S1
где S – площадь рабочей части входного окна, S1 – площадь волнового фронта единичного цуга.
Если же амплитуда заметно меняется на протяжении фронта, то:
m = ∫s1 |A(x,t)|²dxdt / ∫s |A(x,t)|²dxdt /9/
где интегрирование по времени производится в пределах длительности цуга τо , если разрешающее время ∆t >>τо, и в пределах ∆t при условии ∆t<τо .
При этом выражение (4) для вероятности наложений n цугов заменится на выражение для вероятности наложений фотоэлектронов:
PN = (mNf)ⁿ exp(-mNf)/n! = Neⁿ exp(-Ne)/n! /10/
Здесь Ne = mNf – число первичных электронов, выбиваемых с катода фотоумножителя в течение времени ∆t при квантовом выходе катода 100%.
С учетом параметра m соотношение (6) примет вид:
P = mⁿexp(-m)/n! /11/
а вместо (8) получим:
P(n)/P(k) = mR(n-k)[k!/n!] /12/
(R – показатель степени)
Выражение (7) при этом остается справедливым, при условии замены Nf на Nе:
PN(n)/PN(k) = NеR(n-k)[k!/n!] /13/
Таким образом, если свет – совокупность волновых цугов, то амплитудное распределение существенно зависит от параметра m, если же свет – совокупность фотонов как корпускул, то это распределение от параметра m не зависит. В этом и заключается идея experimentum crucis, позволяющего, наконец, решить вопрос о природе света и одновременно вопрос о справедливости копенгагенской интерпретации. Необходимо еще учесть, что квантовая эффективность детектора α на практике всегда значительно меньше 1, так что для получения рабочих формул необходимо в (12) заменить m на αm:
P(n)/P(k)= (αm)R(n-k)[k!/n!] /14/
Выражение (13) при α < 1 остается неизменным, так как первичные фотоэлектроны в этом случае статистически независимы друг от друга и величина квантового выхода на их распределение не влияет (предполагается, что излучение самих световых цугов является вполне стохастическим).
Заметим, что, поскольку при известном угле расхождения волнового цуга величина m есть функция расстояния от источника, то формула (14), если она подтвердится, может быть использована для измерения расстояний.
Предложенная выше экспериментальная схема основана на изучении амплитудного распределения импульсов на выходе детектора, соответствующих разному числу фотоэлектронов от одного единичного цуга.
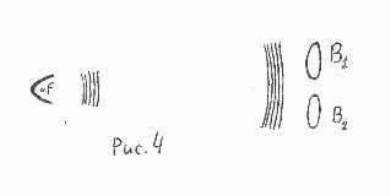
Рассмотрим теперь вариант эксперимента, основанный на одновременной регистрации фотоотсчетов в разных участках волнового фронта единичного цуга. Преимуществом этого варианта является возможность эффективного подавления собственных шумов приемной системы. Расположим два детектора В1 и В2 таким образом, чтобы фронт единичного волнового цуга попадал на оба фотокатода одновременно (рис.4). Выходы детекторов подключим к схеме совпадений с разрешающим временем ∆t.
Вероятность того, что детектор зафиксирует n фотоэлектронов за время ∆t, определяется выражениями (10) или (11) в соответствии с разными гипотезами о природе света. Поскольку акты регистрации на двух детекторах представляют собой независимые события, то вероятность того, что детектор В1 зафиксирует n электронов и за то же время детектор В2 зафиксирует к электронов, в любом случае определяется произведением:
P(n,k)= Pm1(n)Pm2(k) /15/
Взяв отношение:
P(n1,k1)/ P(n2,k2) /16/
для какой-нибудь комбинации чисел n1,k1, n2,k2, получим из (13) и (I4) различающиеся выражения, которые могут быть проверены экспериментально.
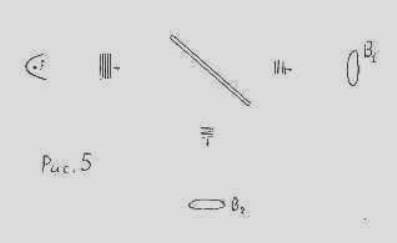
Возможна модификацию последнего варианта, если разделить единичный волновой цуг на две части с помощью полупрозрачной пластинки (рис.5).
Эксперимент, как и в предыдущем случае, основан на сравнении формул (13) и (14). При отсутствии потерь в оптическом тракте можно положить
m1 = m2 = 0,5.
Данная экспериментальная схема напоминает устройство, которое применили в своем опыте Hunbury Brown R. A. Twiss R.Q. [3], изучавшие корреляцию флуктуаций токов фотоумножителей В1 и В2 . Как и опыт Arecchi, этот эксперимент мог бы оказаться решающим, если бы были выполнены два условия: 1)разрешающее время схемы совпадений должно быть много меньше среднего интервала времени между двумя последующими цугами и 2)произведение величин αm не слишком мало. Заметим, что в схеме, показанной на рис.4, можно поставить не два, а несколько детекторов, включенных по схеме совпадений, а в схеме рис.5 можно каждую часть пучка подвергнуть вторичному расщеплению и рассматривать вероятности обнаружения фотоэлектронов, выбитых одним и тем же единичным цугом, одновременно в нескольких детекторах.
Принятие чисто волновой картины не только для фотонного, но и для электронного поля, с необходимостью требует также пересмотра представлений о заряде и массе. Поскольку мы отказались от понятия корпускулы, как носителя энергии, заряда и массы, то вынуждены предположить, что заряд и масса представляют собой характеристики волнового поля, аналогичные частоте, длине волны или поляризации. Эти величины не «размазаны» по объему поля, но в каждой точке поля имеют одно и то же значение (если поле однородно). В качестве таких параметров поля заряд входит в постоянную тонкой структуры, масса – в комптоновскую длину волны или энергию покоя, отношение заряда к массе – в уравнения движения в магнитном поле.
Такое представление о заряде и массе, в сочетании с принципом близкодействия, приводит к выводу о несохранении заряда и массы в единичных взаимодействиях, в полной аналогии с таким же выводом для энергии. С помощью простейшего индикатора единичного заряда – конденсатора Милликена, этот вывод может быть проверен экспериментально.
Пусть электроннооптическая система F(рис.6) испускает единичные цуги электронных волн, поперечник фронта которых соизмерим о диаметром поля наблюдения, охватывающим достаточно большое количество пылинок в камере Милликена К. Электронно-оптическая система снабжена быстродействующим затвором, открывающимся на время ∆t, удовлетворяющее условию: τо <<∆t<<τ, где τо – средняя длительность единичного цуга электронной волны, τ – средний промежуток времени между двумя последовательными цугами. При этом вероятность одновременного попадания двух и более единичных электронных цугов в промежуток времени ∆tможет быть сделана сколь угодно малой, в соответствии с выражением (10).
Промежуток времени между двумя последовательными открываниями затвора должен быть достаточно большим, чтобы можно было надежно зафиксировать движение пылинки, получившей заряд от единичной электронной волны. Поскольку закон сохранения заряда должен остаться справедливым в том же смысле, как и закон сохранения частоты, то каждая пылинка будет всегда получать единичный заряд е.
Примечание 2009 г. Это утверждение сейчас представляется мне неверным, также как неверно представление о передаче нормированного кванта энергии от фотонного к электронному полю. Поэтому неверен и вытекающий отсюда вывод о несохранении заряда в единичных взаимодействиях.
Однако при этом могут быть случаи, когда единичный электронный цуг вызовет появление единичного заряда сразу на нескольких пылинках. Статистика этого явления должна быть такой же, какая была рассмотрена выше для фотонных волн и фотоэлектронов.
В заключение коснемся естественно возникающего вопроса о том, почему нарушение законов сохранения энергии и заряда, если оно имеет место в действительности, не могло быть обнаружено в многочисленных экспериментах по статистической оптике и рассеянию электронов? Единственный ответ мы видим в том, что ни в одном из этих экспериментов не были выполнены одновременно два условия, необходимы для проявления ожидаемого эффекта:
1) ∆t<<τ
2) αm не слишком мало по сравнению с единицей и
3) S1>>So .
Напомним, что, согласно первому условию, единичные волновые цуги должны быть отделены друг от друга промежутком времени, большим по сравнению с разрешающим временем системы регистрации. Второе условие требует, чтобы не была слишком мала эффективность регистрации и не слишком малая часть цуга попадала в окно детектора.
Третье условие заключается в том, что площадь фронта единичного цуга S1 должна быть значительно больше площади единичного взаимодействия So , т.к. только при этом условии на площади S1 могут произойти несколько единичных взаимодействий одновременно. Если же, напротив, имеет место S1<So, то волновой цуг действует как одно целое и ожидаемые эффекты проявиться не могут.
Подавляющая часть экспериментов, в которых наблюдались единичные взаимодействия, имели дело с «электронами» и «фотонами» высоких энергий (частот). В то же время явно имеет место тенденция к сильной локализации волновых пакетов при повышении частоты, что приводит к нарушению условия 2. Если бы удалось искусственно получить, например, фотонные цуги (гамма-кванты) с шириной фронта настолько большой, чтобы происходило рассеяние цуга сразу на большом количестве атомных ядер, при средней частоте цуга, соответствующей энергии рождения пар (Е>1,02 Мэв), то можно было бы наблюдать превращение единичного гамма-кванта сразу в несколько электронно-позитронных пар, в соответствии с описанной выше статистикой. Однако получение таких фотонных цугов, по-видимому, представляет собой практически неразрешимую экспериментальную задачу.
В то же время для низких частот, когда имеют место волновые цуги с широким фронтом, никогда не выполняется второе условие – «нераздробленность» единичного цуга. Это происходит вследствие обязательного применения диафрагм, «вырезающих» очень малую часть цуга. В итоге вероятность появления двух и более фотоэлектронов от единичного цуга, согласно формуле (14) становится чрезвычайно малой и этот эффект маскируется случайными совпадениями фотоэлектронов.
Мы надеемся, что внимание экспериментаторов привлечет тот факт, что основные предпосылки современной квантовой теории: корпускулярный аспект фотонного и электронного полей, а также закон сохранения энергии и заряда в единичных взаимодействиях – не имеют прямого и однозначного экспериментального обоснования.
Ссылки:
1. Schroedinger E. Nuovo Cimento IX, №1, 1958, 162-170
2. Arecchi F.T. Rhys. Rev. Lett. 15, 912 (1965)
3. Hunbury Brown H. and Twiss R.Q. Nature. 177, 27, 1956
Москва, апрель 1972 г.

